[译]Let’s Build A Simple Interpreter. Part 8.

Posted on | Comments:

原文地址：Let’s Build A Simple Interpreter. Part 8.

今天我们会讨论 一元操作符, 也就是一元加(+)/减(-)操作符。

今天的很多材料都是基于前一篇文章中的内容，所以如果你需要复习的话，就回到第七部分 再来一遍。记住：重复是学习之母。

闲话说完，以下是今天要做的事：

  • 扩展语法使它能处理一元加减操作符
  • 增加一个新的 UnaryOp AST 结点类
  • 扩展 parser 使它能生成带有 UnaryOp 结点的 AST
  • 扩展 interpreter 并添加一个新的 visit_UnaryOp 方法来解释一元操作符

让我们开始，好吗？

到现在为止我们只用到了二元操作符(+,-,*,/)，即作用于两个操作数的操作符。

那么什么是一元操作符呢？一元操作符是只作用于一个操作数上的操作符。

下面是一元加减操作符的规则：

  • 一元减(-)操作符返回它数值操作数的相反数
  • 一元加(+)操作符返回它数值操作数的原数
  • 一元操作符的优先级比二元操作符+,-,*,/高

在表达式 “+ - 3” 中第一个 ‘+’ 操作符表示的是一元加操作符，第二个 ‘-’操作符表示了 一元减操作符。表达式 “+ - 3” 等价于 “+ (- (3))” 都等于 -3。你也可以说表达式中的 -3 是一个负整数，但在我们的情况中把它当作一元减操作符，而 3 是它的正整型操作数：

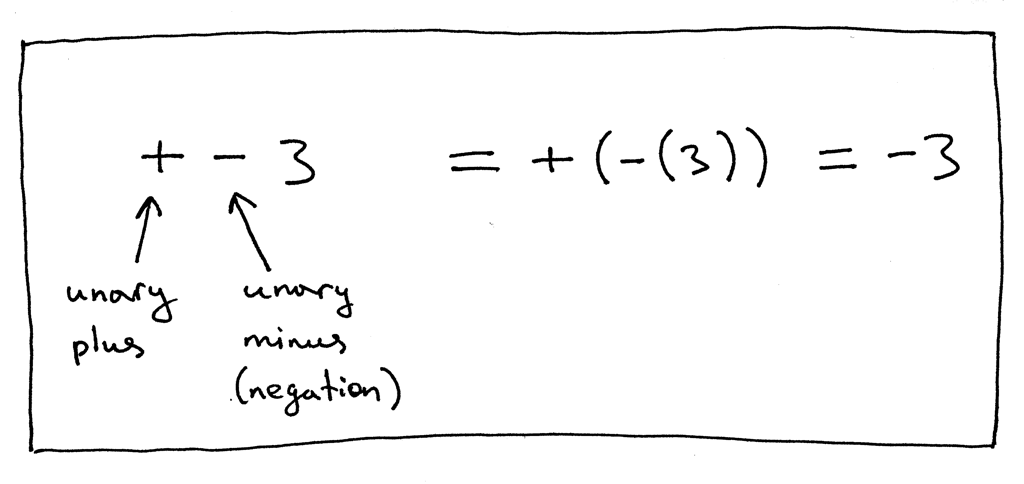
Figure 1: exp1

+ - 3 = + (- (3)) = -3
|  \
 \  unary minus(negation)
  unary plus

让我们再看看另一个表达式，“5 - - 2”:

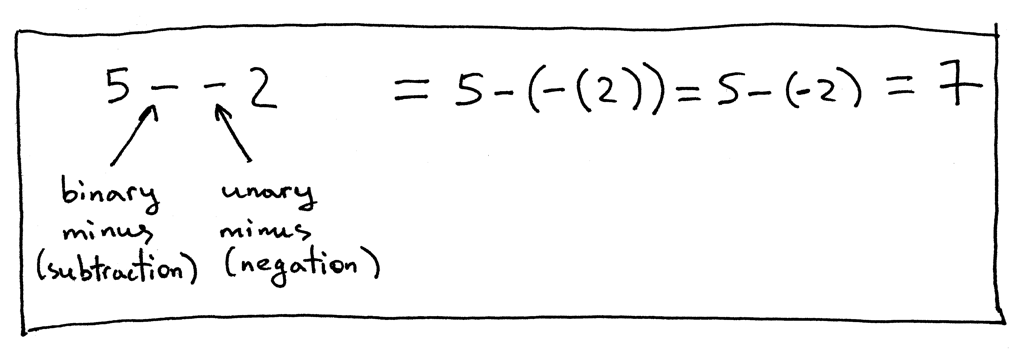
Figure 2: exp2

5 - - 2  = 5 - (- (2)) = 5 - (- 2) = 7
  |  \
   \  unary minus(negation)
    binary minus(subtraction)

在表达式 “5 - - 2” 中第一个 ‘-’ 表示二元减操作符，第二个 ‘-’ 表示一元减操作符， 取相反数操作。

还有一些其他的例子：

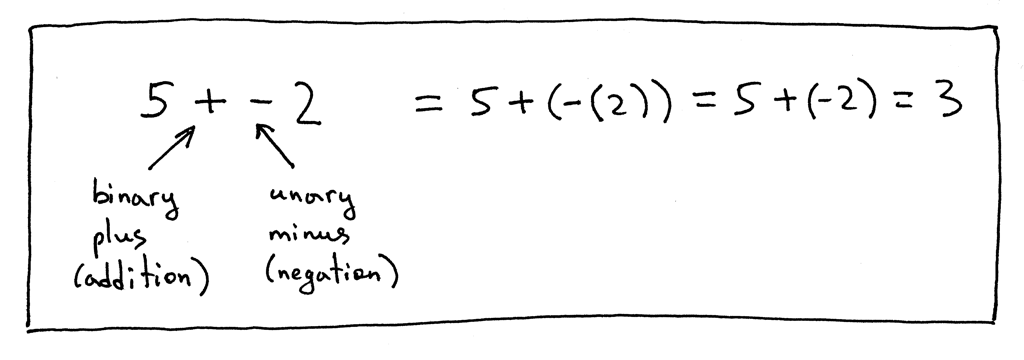
Figure 3: exp3

5 + - 2  = 5 + (- (2)) = 5 + (- 2) = 3
  |  \
   \  unary minus(negation)
    binary plus(addition)

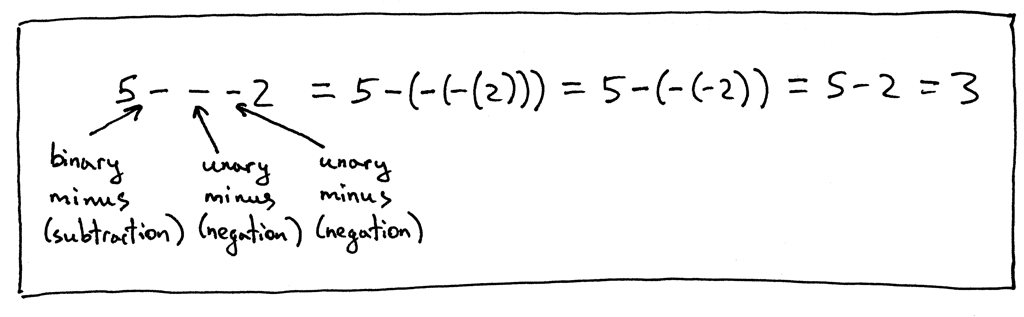
Figure 4: exp4

5 -  -  - 2  = 5 - (- (- (2))) = 5 - (- (2)) = 5 - 2 = 3
  |   \  \
   \   \  unary minus(negation)
    \   unary minus(negation)
     binary plus(addition)

现在让我们更新我们的语法来包含一元加减操作符。我们将会修改 factor 规则来增加一 元操作符，因为一元操作符相比于二元+,-,*,/操作符有更高的优先级。

这是修改前的 factor 规则：

Figure 5: factor before

factor : INTEGER | LPAREN expr RPAREN

而这是我们修改过的 factor 规则，可以处理一元加减操作符：

Figure 6: factor after

factor : (PLUS | MINUS) factor | INTEGER | LPAREN expr RPAREN

如你所见，我扩展了 factor 规则使它引用了自己，这使得我们可以派生出类似 “- - - + - 3” 的表达式，一个包含很多一元操作符的合法表达式。

下面是可以派生出包含一元加减操作符表达式的完整语法：

Figure 7: grammar

expr   : term ((PLUS | MINUS) term)*
term   : factor ((MUL | DIV) factor)*
factor : (PLUS | MINUS) factor | INTEGER | LPAREN expr RPAREN

下一步是添加一个表示一元操作符的 AST 结点类。

这个就可以： 

1
2
3
4
class UnaryOp(AST):
    def __init__(self, op, expr):
	self.token = self.op = op
	self.expr = expr

构造函数有两个参数: op, 表示一元操作符的 token （加或减）, expr, 表示一个 AST 结点。

我们更新后的语法修改了 factor 规则，所以我们需要在 parser 中修改 factor 方法。 我们会在方法中添加处理 “(PLUS | MINUS)” 子规则的代码： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def factor(self):
    """factor : (PLUS | MINUS) factor | INTEGER | LPAREN expr RPAREN"""
    token = self.current.token
    if token.type == PLUS:
	self.eat(PLUS)
	node = UnaryOp(token, self.factor())
	return node
    elif token.type == MINUS:
	self.eat(MINUS)
	node = UnaryOp(token, self.factor())
	return node
    elif token.type == INTEGER:
	self.eat(INTEGER)
	return Num(token)
    elif token.type == LPAREN:
	self.eat(LPAREN)
	node = self.expr()
	self.eat(RPAREN)
	return node

现在我们需要扩展 Interpreter 类，添加一个 visit_UnaryOp 方法来解释一元结点： 

1
2
3
4
5
6
def visit_UnaryOp(self, node):
    op = node.op.type
    if op == PLUS:
	return +self.visit(node.expr)
    elif op == MINUS:
	return -self.visit(node.expr)

断续！

让我们手工建造一个表达式 “5 - - - 2” 的 AST 并把它传递给我们的 interpreter 来验 证新方法 visit_UnaryOp 可以工作。你可以在 Python shell 中这样做： 

1
2
3
4
5
6
7
8
9
10
11
12
13
>>> from spi import BinOp, UnaryOp, Num, MINUS, INTEGER, Token
>>> five_tok = Token(INTEGER, 5)
>>> two_tok = Token(INTEGER, 2)
>>> minus_tok = Token(MINUS, '-')
>>> expr_node = BinOp(
...     Num(five_tok),
...     minus_tok,
...     UnaryOp(minus_token, UnaryOp(minus_token, Num(two_tok)))
... )
>>> from spi import Interpreter
>>> inter = Interpreter(None)
>>> inter.visit(expr_node)
3

上面的语法树看上去是这样的：

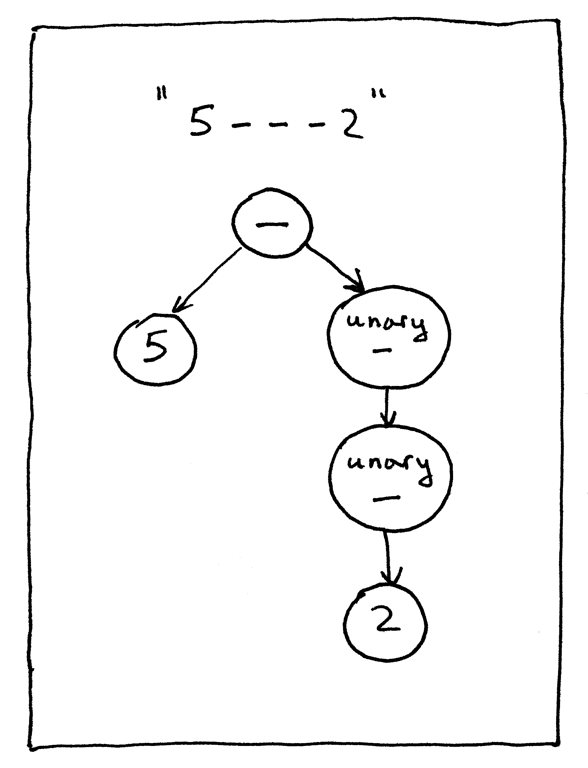
Figure 8: ast

直接从 GitHub 下载本文中 interpreter 的全部源代码。自己试一试，确认修改过的基于 语法树的 interpreter 可以正确地对包含一元操作符的算术表达式求值。

下面是某次运行过程： 

$ python spi.py
spi> - 3
-3
spi> + 3
3
spi> 5 - - - + - 3
8
spi> 5 - - - + - (3 + 4) - +2
10

我还更新了程序 genastdot.py 使得它可以处理一元操作符。下面是一些生成包含一元操作 符表达式生成树图像的例子： 

1
$ python genastdot.py "- 3" > ast.dot && dot -Tpng -o ast.png ast.dot

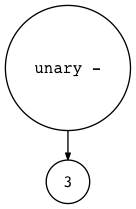
Figure 9: genastdot01

1
$ python genastdot.py "+ 3" > ast.dot && dot -Tpng -o ast.png ast.dot

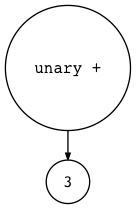
Figure 10: genastdot02

1
$ python genastdot.py "5 - - - + - 3" > ast.dot && dot -Tpng -o ast.png ast.dot

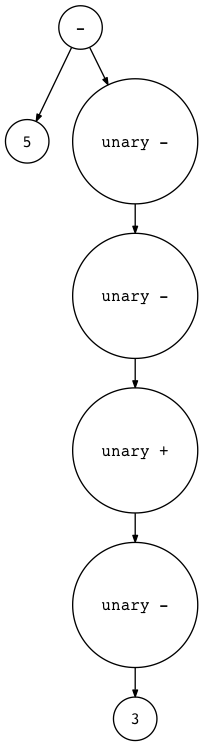
Figure 11: genastdot03

1
$ python genastdot.py "5 - - - + - (3 + 4) - +2" \
  > ast.dot && dot -Tpng -o ast.png ast.dot

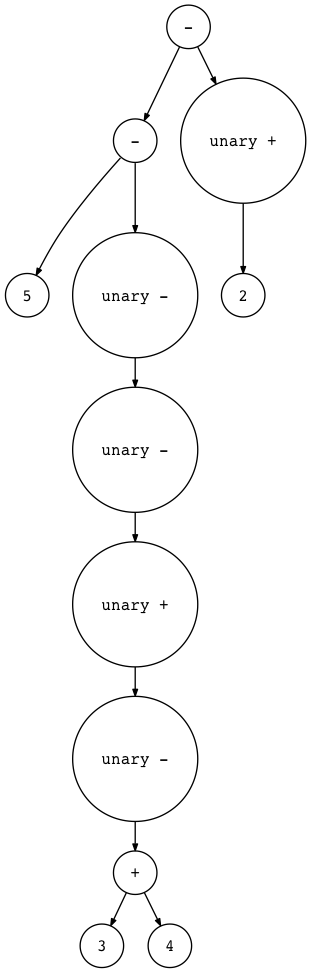
Figure 12: genastdot04

下面是给你的新练习：

Figure 13: exercise

安装 Free Pascal，编译并运行 testunary.pas，验证结果和你的 spi 解释器产生的一样。

这就是今天的所有内容。下一篇文章中，我们会处理赋值语句的问题。敬请关注，下次再见。

下面是我推荐的帮助你学习解释器和编译器的一些书：

  1. Language Implementation Patterns: Create Your Own Domain-Specific and General Programming Languages (Pragmatic Programmers)
  2. Writing Compilers and Interpreters: A Software Engineering Approach
  3. Modern Compiler Implementation in Java
  4. Modern Compiler Design
  5. Compilers: Principles, Techniques, and Tools (2nd Edition)

顺便说一下，我还在写一本书“et’s Build A Web Server: First Steps”，解释了怎么从头 写一个基本的 Web 服务器。你可以从这里， 这里 和 这里 来感受一下这本书。

本系列的所有文章：

Last Updated 2018-05-26 Sat 14:12.
Render by hexo-renderer-org with Emacs 25.2.2 (Org mode 9.1.13)
0%