[译]Let’s Build A Simple Interpreter. Part 5.

原文地址：Let’s Build A Simple Interpreter. Part 5.

怎么解决像怎么创建一个解释器或编译器这样复杂的问题呢？起初这个问题看上去像是需要 把一个乱糟糟的线团解成一个完美的线球。

方法其实就是一条线、一个结地解。尽管有时你可能会觉得你不会立即理解某一点，但你一 定要继续前进。如果你足够坚持，最终一定会“开窍”的，我保证（天呐，如果我每次不能马 上理解一件事都存25美分的话早就成富人了：）。

也许在理解怎么新建一个解释器和编译器这件事上，我可以给你的最好建议是，读文章中的 解释，读代码，然后自己写代码，就算是在一段时间内把相同的代码写很多遍也要让这些素 材和代码变得对你来说很自然，只有到此时才开始学习新的主题。不要着急，慢下来花些时 间把基础的概念理解的深一些。这个方式，虽然看起来很慢，会在以后回报丰厚的。相信我。

你最终一定会得到你完美的线球的。而且，知道吗？即使它不那么完美也比另一种结果好， 即什么也不做，不学这个主题或快速地浏览一下然后在几天内忘掉。

记住──不要停止拆解：一次一条线、一个结，通过代码，很多代码，练习你学到的东西：

Figure 1: ball of yarn

今天你会所有从本系列以前文章中学到的知识，并学习如何解析和解释包含任意数量加减乘 除运算符的算术表达式。你会写一个能够对“14 + 2 * 3 - 6 / 2”这样的表达式进行求值的 解释器。

在开始深入及写代码之前让我们聊聊操作符的 结合性 和 优先级.

按照惯例 7 + 3 + 1 等价于 (7 + 3) + 1, 7 - 3 - 1 等价于 (7 - 3) - 1. 没什么特殊 的。我们学到的都是这样并把它当作理所当然的。如果我们把 7 - 3 - 1 当作 7 - (3 - 1) 的话结果就是 5 而不是 3 了。

在平常的算术及大多数编程语言中加减乘除都是左结合的：

7 + 3 + 1 is equivalent to (7 + 3) + 1
7 - 3 - 1 is equivalent to (7 - 3) - 1
8 * 4 * 2 is equivalent to (8 * 4) * 2
8 / 4 / 2 is equivalent to (8 / 4) / 2

一个运算符是左结合的是什么意思呢？

当一个操作数（比如 7+3+1 中的 3）两边都有加号时，我们需要一个规则来决定哪个运算 符作用于 3. 是 3 左边的还是右边的呢？操作符 + 是左结合的原因是当一个操作数两边都 有加号时，该操作数属于左边的操作符。这就是根据惯例 7 + 3 + 1 等价于 (7 + 3) + 1 的原因。

那么，像 7 + 5 * 2 中的 5 这样两边有不同的操作符的表达式呢？表达式是等价于 7 + (5 * 2) 还是 (7 + 5) * 2 呢？我们怎么解决这个歧义呢？

在这种情况下，结合性惯例帮不了我们因为它只能在一种操作符下使用，要么是加法性的 (+,-)要么是乘法性的(*,/)。我们需要另一个惯例来解决一个表达式中存在不同的操作符时 的歧义。我们需要一个惯例来定义运算符的优先级。

就是下面这样：我们说如果运算符*比+先取运算符，它就有较高的优先级。在我们知道和使 用的算术中，乘除的优先级比加减高。结果就是 7 + 5 * 2 等价于 7 + (5 * 2) 而 7 - 8 / 4 等价于 7 - (8 / 4)。

在一个表达式中有相同优先级的运算符出现时，我们就使用结合性惯例从左到右执行：

7 + 3 - 1 is equivalent to (7 + 3) - 1
8 / 4 * 2 is equivalent to (8 / 4) * 2

我希望你不要认为谈论这么多运算符的结合性和优先级是想把你无聊死。关于这些惯例的一 个好处就是，可以从一个表示结合性和优先级的表中构建出算术表达式的语法。然后，我们 就可以使用第四部分中的准则把语法翻译成代码，我们的解释器就可以在结合性的基础上处 理优先级。

好，下面是我们的优先级表：

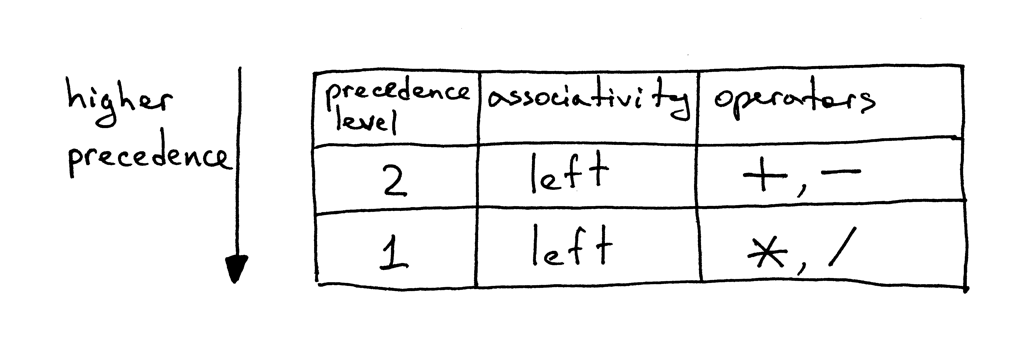
Figure 2: precedence

	优先级	结合性	运算符
低	2	left	+,-
高	1	left	*,/

从表中可知，操作符加减有相同的优先级而且都是左结合的。还可以看到乘除也是左结合且 有相同的优先级，但比加减有更高的优先级。

下面是怎么从优先级表中构建语法：

1. 对于每一个优先级定义一个非终结符。这个非终结符的生成式的 body 应该由本优先级 的算术运算符和更高优先级的非终结符组成。
2. 对表达式的基本单元(在我们的例子中是 INTEGER)新建一个额外的非终结符 factor. 一般原则就是如果你有 N 级优先级，你一共会需要 N+1 非终结符：每个优先级一个再 加上基本单元的一个。

继续！

让我们遵循这些规则来构建我们的语法。

根据规则1我们会定义两个非终结符：对应优先级2的非终结符叫做 expr, 对应优先级1的 非终结符叫做 term. 根据规则2我们会为算术表达式的基本单元（整数）定义一个非终结 符 factor.

我们新语法的开始符号会是 expr 且其产生式的 body 会包含优先级2的操作符（在这里 是+、-）的使用，还会包含优先级更高的非终结符 term:

Figure 3: expr

expr : term ((PLUS | MINUS) term)*

产生式 term 的 body 会包含优先级1的操作符（在这里是*、/）的使用，还会包含表示 算术表达式基本单元，整数，的非终结符 factor:

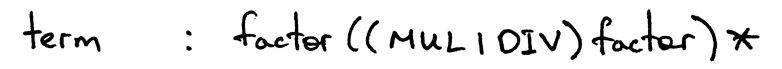
Figure 4: term

term : factor ((MUL | DIV) factor)*

非终结符 factor 的产生式则为：

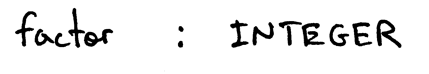
Figure 5: factor

factor : INTEGER

你已经在前面的文章中的语法和句法图中见过上面的产生式作为一部分出现，但在这我们把 它们结合到一个语法中，它会处理好操作符的结合性和优先级的：

Figure 6: grammar

expr   : term   ((ADD | MINUS) term)*
term   : factor ((MUL | DIV) factor)*
factor : INTEGER

下面是上面语法相应的句法图：

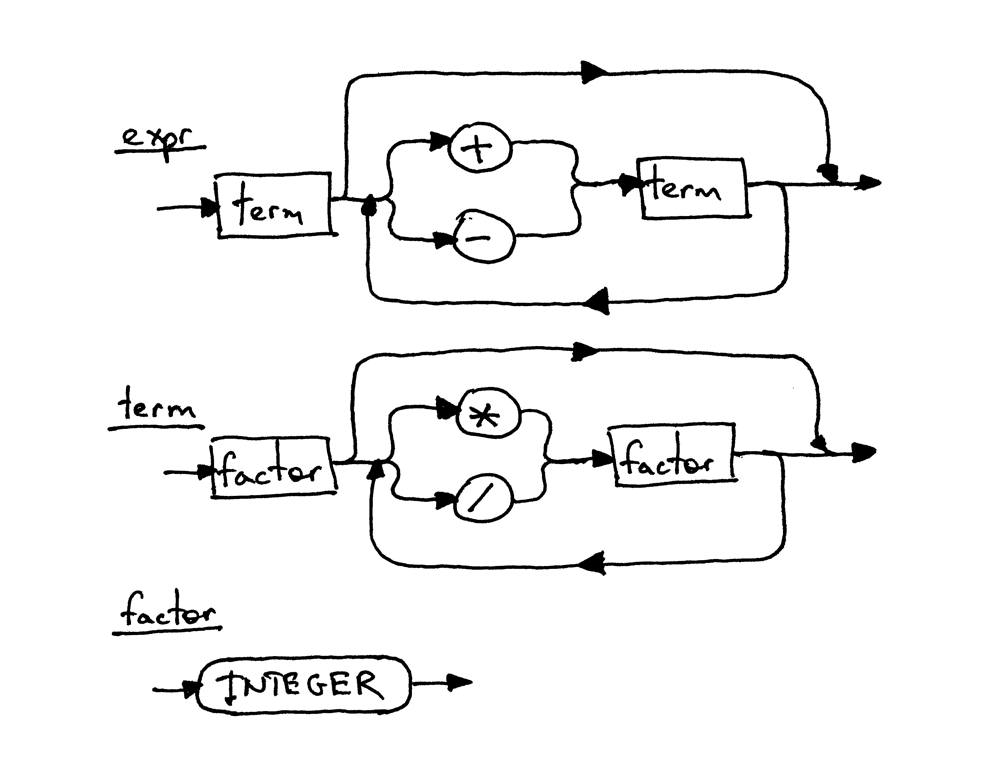
Figure 7: syntax diagram

图中每个矩形都是一个其他句法图的“函数调用”。如果你以表达式 7 + 5 * 2 为例并从顶 层图 expr 开始逐步分解到最底层的图 factor, 你应该可以看到位于中间的图的高优 先级操作符*和/会比上面的图的操作符+和-先执行。

为了解释清楚运算符的优先级，让我们看看使用上面语法和句法图来分解相同算术表达式 7 + 5 * 2 的过程。这只是另一种展示高优先级运算符先于低优先级运算符执行这个事实的 方式。

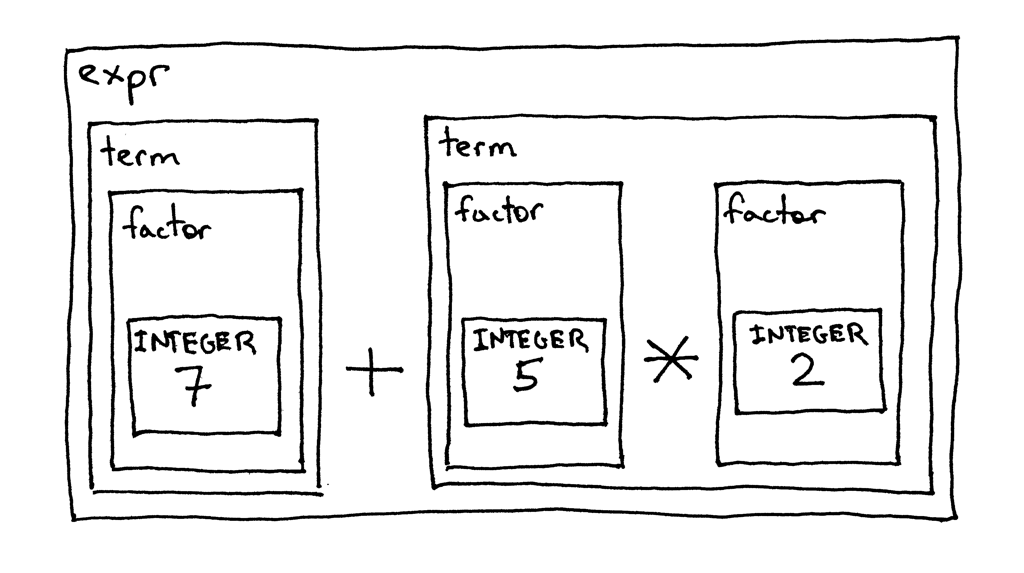
Figure 8: expression decomposition

好了，让我们使用第四部分中的准则把该语法转化成代码，看看它怎么工作，好吗？

现看一下这张图：

Figure 9: grammar

下面是能处理可以包含任意数量加减乘除操作符的算术表达式的计算器的完整代码。

相比于第四部分代码的主要变化有：

• Lexer 类现在可以把+,-,*和/都 token 化了（没什么新方法，我们只是把前面文章中 的代码合并到一个类中来支持所有这些 token）
• 回想语法中的每条规则（生成式）R都要变成一个同名的方法，且对该规则的引用都要变 成一个方法调用 R() 这一点。现在 Interpreter 类有了三个方法来对应语法中的非 终结符： expr, term, factor.

源代码：

# Token types
#
# EOF (end-of-file) token is used to indicate that
# there is no more input left for lexical analysis
INTEGER, PLUS, MINUS, MUL, DIV, EOF = (
    'INTEGER', 'PLUS', 'MINUS', 'MUL', 'DIV', 'EOF'
)

class Token():
    def __init__(self, type, value):
	# token type: INTEGER, PLUS, MINUS, MUL, DIV, or EOF
	self.type = type
	# token value: non-negative integer value, '+', '-', '*', '/', or None
	self.value = value

    def __str__(self):
	"""String representation of the class instance.	Examples:	    Token(INTEGER, 3)	    Token(PLUS, '+')	    Token(MUL, '*')	"""

	Examples:
	    Token(INTEGER, 3)
	    Token(PLUS, '+')
	    Token(MUL, '*')
	"""
	return f'Token({self.type}, {repr(self.value)})'

    def __repr__(self):
	return self.__str__()

class Lexer():
    def __init__(self, text):
	# client string input, e.g. "3 * 5", "12 / 3 * 4", etc
	self.text = text
	# self.pos is an index into self.text
	self.pos = 0
	self.current_char = self.text[self.pos]

    def error(self):
	raise Exception('Lexer error')

    def advance(self):
	"""Advance the `pos` pointer and set the `current_char` variable."""
	self.pos += 1
	if self.pos >= len(self.text):
	    self.current_char = None  # Indicates end of input
	else:
	    self.current_char = self.text[self.pos]

    def skip_whitespace(self):
	while self.current_char is not None and self.current_char.isspace():
	    self.advance()

    def integer(self):
	"""Return a (multidigit) integer consumed from the input."""
	value = ''
	while self.current_char is not None and self.current_char.isdigit():
	    value += self.current_char
	    self.advance()
	return int(value)

    def get_next_token(self):
	"""Lexical analyzer (also known as scanner or tokenizer)	This method is responsible for breaking a sentence	apart into tokens. One token at a time.	"""

	This method is responsible for breaking a sentence
	apart into tokens. One token at a time.
	"""
	while self.current_char is not None:
	    if self.current_char.isspace():
		self.skip_whitespace()
		continue
	    elif self.current_char.isdigit():
		return Token(INTEGER, self.integer())
	    elif self.current_char == '*':
		self.advance()
		return Token(MUL, '*')
	    elif self.current_char == '/':
		self.advance()
		return Token(DIV, '/')
	    elif self.current_char == '+':
		self.advance()
		return Token(PLUS, '+')
	    elif self.current_char == '-':
		self.advance()
		return Token(MINUS, '-')
	    else:
		self.error()
	return Token(EOF, None)

class Interpreter():
    def __init__(self, lexer):
	self.lexer = lexer
	# set current token to the first token taken from the input
	self.current_token = self.lexer.get_next_token()

    def error(self):
	raise Exception('Interpreter error')

    def eat(self, token_type):
	# compare the current token type with the passed token
	# type and if they match then "eat" the current token
	# and assign the next token to the self.current_token,
	# otherwise raise an exception.
	if self.current_token.type == token_type:
	    self.current_token = self.lexer.get_next_token()
	else:
	    self.error()

    def factor(self):
	"""factor : INTEGER"""
	value = self.current_token.value
	self.eat(INTEGER)
	return value

    def term(self):
	"""term : factor ((MUL | DIV) factor)*"""
	value = self.factor()

	while self.current_token.type in (MUL, DIV):
	    if self.current_token.type == MUL:
		self.eat(MUL)
		value *= self.factor()
	    elif self.current_token.type == DIV:
		self.eat(DIV)
		value /= self.factor()
	return value

    def expr(self):
	"""Arithmetic expression parser / interpreter.	calc>  14 + 2 * 3 - 6 / 2	17	expr   : term ((PLUS | MINUS) term)*	term   : factor ((MUL | DIV) factor)*	factor : INTEGER	"""

	calc>  14 + 2 * 3 - 6 / 2
	17

	expr   : term ((PLUS | MINUS) term)*
	term   : factor ((MUL | DIV) factor)*
	factor : INTEGER
	"""
	value = self.term()

	while self.current_token.type in (PLUS, MINUS):
	    if self.current_token.type == PLUS:
		self.eat(PLUS)
		value += self.term()
	    elif self.current_token.type == MINUS:
		self.eat(MINUS)
		value -= self.term()
	return value

    def parse(self):
	return self.expr()

def main():
    while True:
	try:
	    text = input('calc> ')
	except EOFError:
	    print()
	    break

	if len(text.strip()):
	    interpreter = Interpreter(Lexer(text))
	    result = interpreter.parse()
	    print(result)
	else:
	    continue

if __name__ == '__main__':
    main()

将以上代码保存到名为 calc5.py 中，或者直接从 GitHub 上下载。和以往一样，自己尝 试一下，确认解释器可以对包含不同优先级操作符的算术表达式进行求值。

下面是在我笔记本上的一次尝试：

$ python calc5.py
calc> 3
3
calc> 2 + 7 * 4
30
calc> 7 - 8 / 4
5
calc> 14 + 2 * 3 - 6 / 2
17

下面是今天的新练习：

Figure 10: exercises

• 根据本文的描述凭记忆写出一个解释器，不要参考文中的代码。为你的解释器写一些测试， 确保它们可以通过。
• 扩展这个解释器来处理包含括号的算术表达式，使得你的解释器可以对嵌套很深很深的算 术表达式进行求值如：7 + 3 * (10 / (12 / (3 + 1) - 1))

检查你的理解。

1. 一个操作符是左结合的是什么意思？
2. 操作符加减是左结合的还是右结合的？乘除呢？
3. 操作符加是否比操作符乘有更高的优先级？

哈，你从头读到了尾！这真的很不容易。我下次回来会带来一篇新文章──保持关注，聪明点， 和往常一样也别忘了做练习。

下面是我推荐的帮助你学习解释器和编译器的一些书：

1. Language Implementation Patterns: Create Your Own Domain-Specific and General Programming Languages (Pragmatic Programmers)
2. Writing Compilers and Interpreters: A Software Engineering Approach
3. Modern Compiler Implementation in Java
4. Modern Compiler Design
5. Compilers: Principles, Techniques, and Tools (2nd Edition)

顺便说一下，我还在写一本书“et’s Build A Web Server: First Steps”，解释了怎么从头 写一个基本的 Web 服务器。你可以从这里， 这里 和 这里 来感受一下这本书。

本系列的所有文章：

• Let’s Build A Simple Interpreter. Part 1.
• Let’s Build A Simple Interpreter. Part 2.
• Let’s Build A Simple Interpreter. Part 3.
• Let’s Build A Simple Interpreter. Part 4.
• Let’s Build A Simple Interpreter. Part 5.
• Let’s Build A Simple Interpreter. Part 6.
• Let’s Build A Simple Interpreter. Part 7.
• Let’s Build A Simple Interpreter. Part 8.
• Let’s Build A Simple Interpreter. Part 9.
• Let’s Build A Simple Interpreter. Part 10.
• Let’s Build A Simple Interpreter. Part 11.
• Let’s Build A Simple Interpreter. Part 12.
• Let’s Build A Simple Interpreter. Part 13.
• Let’s Build A Simple Interpreter. Part 14.

Last Updated 2018-05-26 Sat 14:12.
Render by hexo-renderer-org with Emacs 25.2.2 (Org mode 9.1.13)