[译]Let’s Build A Simple Interpreter. Part 4.

Posted on | Comments:

原文地址：Let’s Build A Simple Interpreter. Part 4.

你是被动地学习这些文章中的内容呢，还是主动地练习呢？我希望你在积极练习。真的:)

记得孔子说过什么吗？

听而易忘

Figure 1: confucius hear

见而易记

Figure 2: confucius see

做而易懂

Figure 3: confucius do

在前面的文章中你学会了怎样识别和解释包含任意数量的加减操作的算术表达式，例如“7 - 3 + 2 - 1”。还学会了句法图以及它们如何被用来表示一门编程语言的语法。

今天你将会学习解析(parse)和解释(interpret)包含任意乘除操作的算术表达式，例如“7 * 4 / 2 * 3”。在这篇文章中使用的是整数除法，所以对于表达式“9 / 4”来说，结果是一个 整数：2。

我今天会讲很多另一个表示编程语言句法的广泛使用的表示法，叫 上下文无关语法 (context-free grammars, 简记为 grammars)或 BNF (Backus-Naur Form)。为了这篇文 章的目的，我不会使用纯 BNF 记法，而更像是一个修改过的 EBNF 记法。

以下是一些使用语法的原因：

  1. 语法使用了一种简明的方式来描述一门编程语言的句法。不像句法图，语法非常紧凑。 在以后的文章中，你会看到我越来越多地使用语法。
  2. 语法可以做为文档保存。
  3. 即使对从头开始写解析器(parser)来说，语法也是一个好的入手点。很多时候通过遵循 一套简单的规则你就可以把语法转化成代码。
  4. 有一套工具，叫解析器生成器(parser generator)，可以把语法做为输入并自动根据它 为你生成一个解析器。我会以后在这个系列中谈到这些工具。

现在，我们来聊聊语法的机制方面，好吗？

下面的语法描述了算术表达式，像“7 * 4 / 2 * 3”这样的（这只是该语法可以生成的许多 表达式之一）：

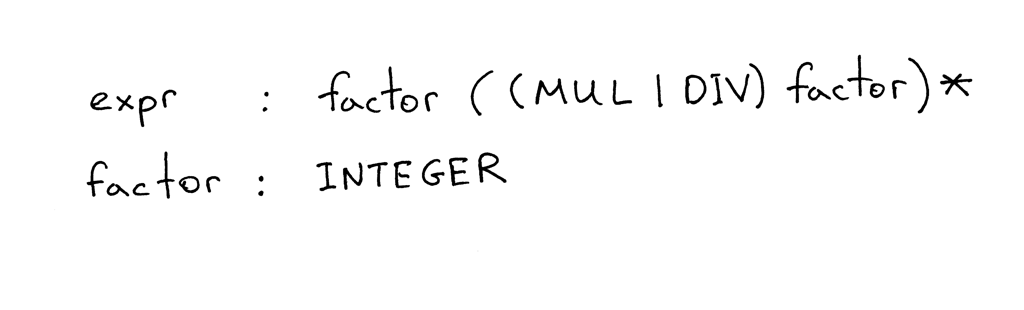
Figure 4: bnf1

expr : factor ((MUL|DIV) factor)* factor : INTEGER

语法是由一系列规则组成的，也被称为产生式(production)。我们的语法中有两条规则：

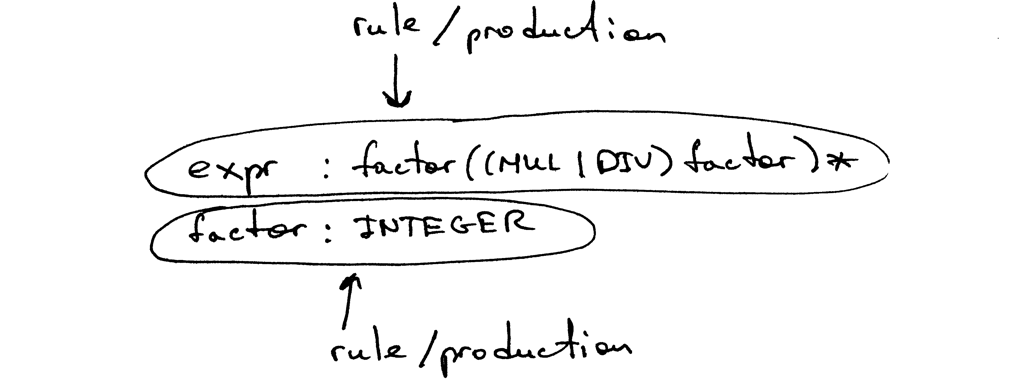
Figure 5: bnf2

一条规则由一个非终结符(叫做 head 或 生成式的 左边)，一个分号，和一系列终结 符和/或非终结符(叫做 body 或 右边)：

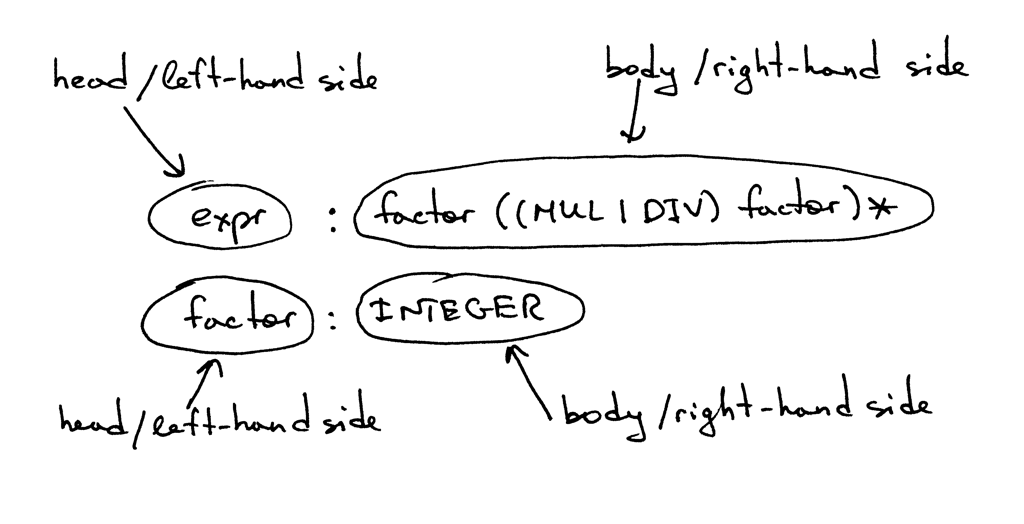
Figure 6: bnf3

expr   : factor ((MUL|DIV) factor)*
factor : INTEGER
------   --------------------------
  \          `head/left-hand side
   `head/left-hand side

在上面展示的语法中，像 MUL, DIV, 或 INTEGER 这样的 token 被称为 终结符, expr factor 这样的变量被称为 非终结符.

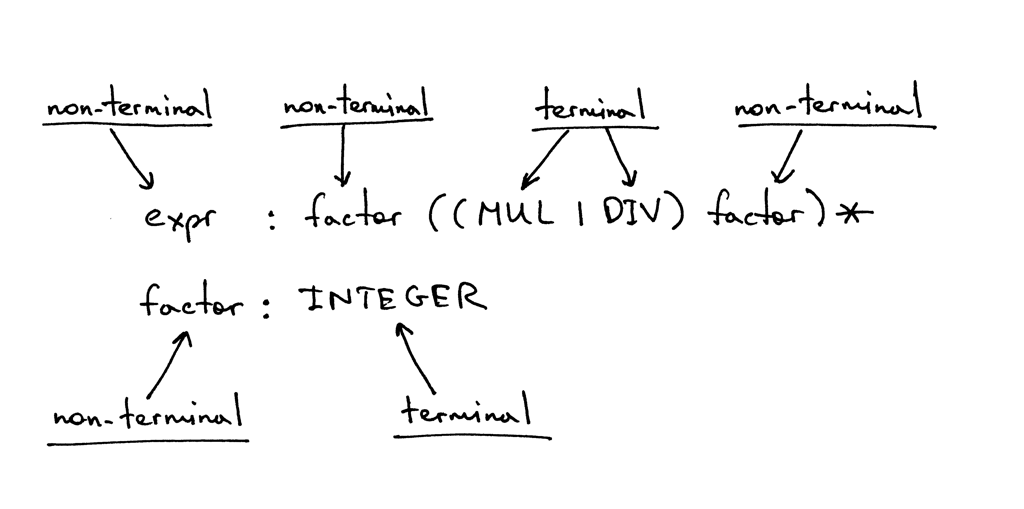
Figure 7: bnf4

non-terminal terminal non-terminal / \ / \ / -— -–— — — -–— expr : factor ((MUL|DIV) factor)* factor : INTEGER -–— --–— \ \ non-terminal terminal

第一条规则左边的非终结符被叫做 开始符号. 在我们的语法中，开始符号是 expr:

Figure 8: bnf5

 start symbol
----
expr   : factor ((MUL|DIV) factor)*
factor : INTEGER

你可以这么 expr 这条读规则“expr 是一个 factor 后面可选地跟一个乘或除运算符再跟 另一个 factor，后面也相应可选地跟一个乘或除运算符再跟另一个 factor，如此重复”。

factor 是什么？对于本文来说 factor 就是一个整数。

让我们快速地过一遍语法中的符号及它们的意义。

|
多选一。竖线表示“或”。所以 (MUL | DIV) 表示 MUL 或 DIV
(...)
被括号包围表示把终结符和/或非终结符组成一组，就像 (MUL | DIV)
(...)*
分组中的内容被匹配 0 或多次

如果你以前用过正则表达式，那应该对 |, (), (...)* 这些符号很熟悉。

语法通过解释可以组成什么样的句子来定义一门语言。你通过语法派生出算术表达式的方式 为：首先从开始符号 expr 开始，然后反复地使用所包含的非终结符的规则替换该终结符， 直到生成一个只包含终结符的句子。语法能组成的句子构成了一门语言。

如果该语法不能派生出某个特定的算术表达式，那么它就不支持该表达式，当它试着对该表 达式进行识别时将会产生一个句法错误。

我觉得该举些例子了。下面是语法如何派生出表达式 3:

Figure 9: derive1

expr
factor ((MUL|DIV) factor)*
factor
INTEGER
3

下面是语法如何派生出表达式 3 * 7:

Figure 10: derive2

expr
factor ((MUL|DIV) factor)*
factor MUL factor
 3      *   7

下面是语法如何派生出表达式 3 * 7 / 2:

Figure 11: derive3

expr
factor ((MUL|DIV) factor)*
factor MUL factor ((MUL|DIV) factor)*
factor MUL factor DIV factor
 3      *   7      /   2

哇，好多理论啊！

当我第一次读到语法，相关术语，以及所以这些东西时，我是下面这种感觉：

Figure 12: bnf hmm

我可以向你保证我绝不是这样的：

Figure 13: bnf yes

我花了一些时间才熟悉这些表示方法，它们怎么工作，以及它们跟 parser 和 lexer 的关 系，但我可以告诉你从长期来看是值得的，因为在实际和编译器书籍中它的应用很广泛，在 某一时刻你一定会用到的。那么，为什么不早点接触呢？

现在，让我们把语法变成代码，好吗？

下面是一些我们在把语法转化成源代码时会用到的准则。按照这些准则，你真的就可以把语 法翻译成一个可工作的 parser:

  1. 对于语法中定义的每个规则 R，将它做成一个有相同名字的方法，对该规则的引用就变 成了一个方法调用：R()。该方法的方法体遵循该规则的步骤，过程中使用相同的准则。
  2. 多选一 (a1|a2|aN) 变成 if-elif-else 语句
  3. 可选组 (...)* 变成一个可以执行 0 或多次的 while 循环
  4. 每个 Token 引用 T 变成一个 eat 方法调用: eat(T). eat 方法的工作是当它匹 配到当前的 向前看 (lookahead) token 就消耗掉它，然后从 lexer 中得到一个新 token 并将它赋值给内部变量 currenttoken.

这些准则看上去像这样：

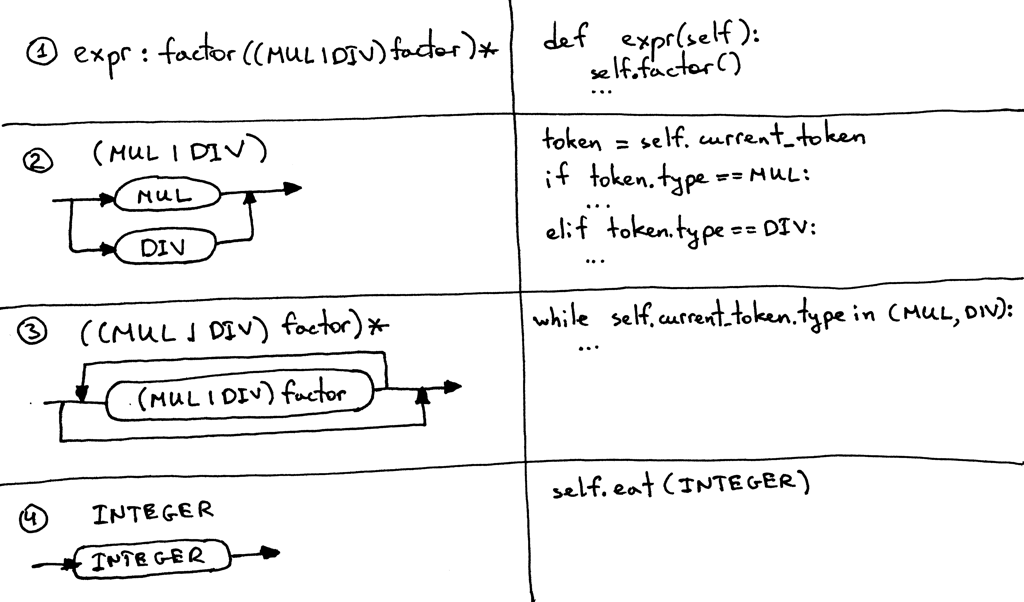
Figure 14: rules

让我们继续并遵循上述准则把我们的语法转化为代码。

我们的语法中有两条规则： expr 和 factor. 我们从 factor 规则（生成式）开始。 根据准则，需要新建一个名为 factor 的方法（规则1)，它调用了一次 eat 方法来消耗 token INTEGER（准则4)： 

1
2
def factor(self):
    self.eat(INTEGER)

很简单，不是吗？

继续！

expr 规则变成了 expr 方法（两次提醒遵循了准则1）。规则体开始的 factor 引用 变成了对 factor() 方法的调用。可行组 (...)* 变成了一个 while 循环，多选一 (MUL|DIV) 变成了一个 if-elif-else 语句。把这些片段合并在一起就得到了下面的 expr 方法： 

1
2
3
4
5
6
7
8
9
10
11
def expr(self):
    self.factor()

    while self.current_token.type in (MUL, DIV):
	token = self.current_token
	if token.type == MUL:
	    self.eat(MUL)
	    self.factor()
	elif token.type == DIV:
	    self.eat(DIV)
	    self.factor()

请花点时间并学习我是怎么把语法转化成源代码的。确保你理解了该部分，因为稍后就会派 上用场。

为了你查看方便，我把上面的代码放在了文件 parser.py 中，它包含了 lexer 和 parser 但没有 interpreter。你可以直接从 GitHub 下载并尝试一下。它包含有一个 interpreter 提示符，你可以输入表达式来查看它是否合法，即查看根据语法建立的 parser 是否可以识别出表达式。

下面是在我笔记本上的一次尝试： 

$ python parser.py
calc> 3
calc> 3 * 7
calc> 3 * 7 / 2
calc> 3 *
Traceback (most recent call last):
  File "parser.py", line 155, in <module>
    main()
  File "parser.py", line 151, in main
    parser.parse()
  File "parser.py", line 136, in parse
    self.expr()
  File "parser.py", line 130, in expr
    self.factor()
  File "parser.py", line 114, in factor
    self.eat(INTEGER)
  File "parser.py", line 107, in eat
    self.error()
  File "parser.py", line 97, in error
    raise Exception('Invalid syntax')
Exception: Invalid syntax

尝试一下！

我忍不住还要提句法图。这是相同的 expr 规则对应的句法图：

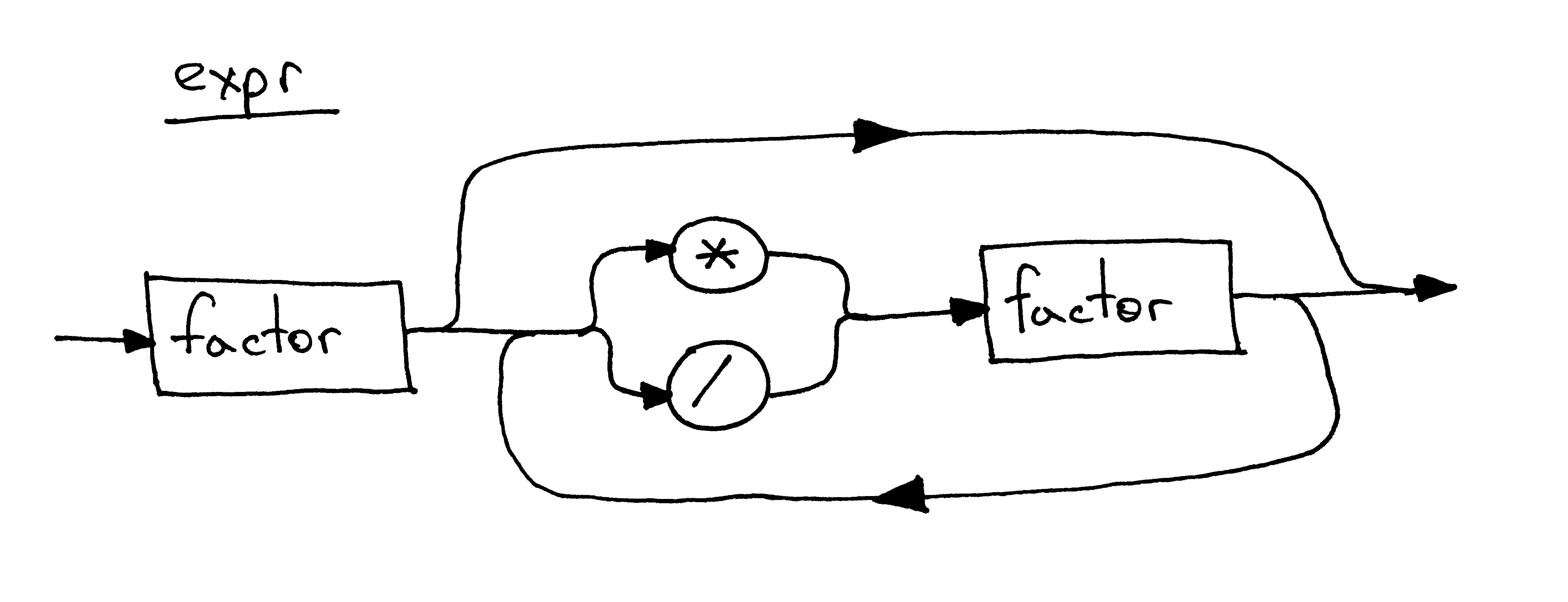
Figure 15: syntax diagram

是时候一头钻进我们新算术表达式解释器的源代码里了。下面是可以处理包含任意数量整数 乘除（整数除法）操作的合法的算术表达式的计算器代码。你可以看到我把词法分析器重构 到了一个单独的类 Lexer 中，并让 Interpreter 类使用 Lexer 实例做为参数： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
# Token types
#
# EOF (end-of-file) token is used to indicate that
# there is no more input left for lexical analysis
INTEGER, MUL, DIV, EOF = 'INTEGER', 'MUL', 'DIV', 'EOF'

class Token():
    def __init__(self, type, value):
	# token type: INTEGER, MUL, DIV, or EOF
	self.type = type
	# token value: non-negative integer value, '*', '/', or None
	self.value = value

    def __str__(self):
	"""String representation of the class instance.

	Examples:
	    Token(INTEGER, 3)
	    Token(MUL, '*')
	"""
	return f'Token({self.type}, {repr(self.value)})'

    def __repr__(self):
	return self.__str__()

class Lexer():
    def __init__(self, text):
	# client string input, e.g. "3 * 5", "12 / 3 * 4", etc
	self.text = text
	# self.pos is an index into self.text
	self.pos = 0
	self.current_char = self.text[self.pos]

    def error(self):
	raise Exception('Parse error')

    def advance(self):
	"""Advance the `pos` pointer and set the `current_char` variable."""
	self.pos += 1
	if self.pos < len(self.text):
	    self.current_char = self.text[self.pos]
	else:
	    self.current_char = None

    def skip_whitespace(self):
	while self.current_char is not None and self.current_char.isspace():
	    self.advance()

    def integer(self):
	"""Return a (multidigit) integer consumed from the input."""
	value = ''
	while self.current_char is not None and self.current_char.isdigit():
	    value += self.current_char
	    self.advance()
	return int(value)

    def get_next_token(self):
	"""Lexical analyzer (also known as scanner or tokenizer)

	This method is responsible for breaking a sentence
	apart into tokens. One token at a time.
	"""
	while self.current_char is not None:
	    if self.current_char.isspace():
		self.skip_whitespace()
		continue
	    elif self.current_char.isdigit():
		return Token(INTEGER, self.integer())
	    elif self.current_char == '*':
		self.advance()
		return Token(MUL, '*')
	    elif self.current_char == '/':
		self.advance()
		return Token(DIV, '/')
	    else:
		self.error()
	return Token(EOF, None)

class Interpreter():
    def __init__(self, lexer):
	self.lexer = lexer
	# set current token to the first token taken from the input
	self.current_token = self.lexer.get_next_token()

    def error(self):
	raise Exception('Interpret error')

    def eat(self, token_type):
	# compare the current token type with the passed token
	# type and if they match then "eat" the current token
	# and assign the next token to the self.current_token,
	# otherwise raise an exception.
	if self.current_token.type == token_type:
	    self.current_token = self.lexer.get_next_token()
	else:
	    self.error()

    def factor(self):
	"""Return an INTEGER token value.

	factor : INTEGER
	"""
	token = self.current_token
	self.eat(INTEGER)
	return token.value

    def expr(self):
	"""Arithmetic expression parser / interpreter.

	expr   : factor ((MUL | DIV) factor)*
	factor : INTEGER
	"""
	value = self.factor()

	while self.current_token.type in (MUL, DIV):
	    token_type = self.current_token.type
	    if token_type == MUL:
		self.eat(MUL)
		value *= self.factor()
	    elif token_type == DIV:
		self.eat(DIV)
		value /= self.factor()
	return value

    def parse(self):
	return self.expr()

def main():
    while True:
	try:
	    text = input('calc> ')
	except EOFError:
	    print()
	    break

	if len(text.strip()):
	    interpreter = Interpreter(Lexer(text))
	    result = interpreter.parse()
	    print(result)

if __name__ == '__main__':
    main()

将以上代码保存到名为 calc4.py 中，或者直接从 GitHub 上下载。和以往一样，自己尝 试一下，确认它能工作。

下面是在我笔记本上的一次尝试： 

$ python calc4.py
calc> 7 * 4 / 2
14
calc> 7 * 4 / 2 * 3
42
calc> 10 * 4  * 2 * 3 / 8
30

我知道你已经等不及了:) 下面是今天的新练习：

Figure 16: exercises

  • 写一个语法来描述包含任意数量的 +, -, *, 或 / 操作符的算术表达式。这个语法需要 能够派生出像 “2 + 7 * 4”, “7 - 8 / 4”, “14 + 2 * 3 - 6 / 2” 等等这样的表达式。
  • 使用这个语法，写一个可以对包含任意数量的 +, -, *, 或 / 操作符的算术表达式求值 的解释器。你们解释器需要能够处理像 “2 + 7 * 4”, “7 - 8 / 4”, “14 + 2 * 3 - 6 / 2” 等等这样的表达式。
  • 如果你完成了上面的练习，放松好好享受一下:)

检查你的理解。

记住今天文章中的语法，回答下面的问题，需要时参考以下的图片：

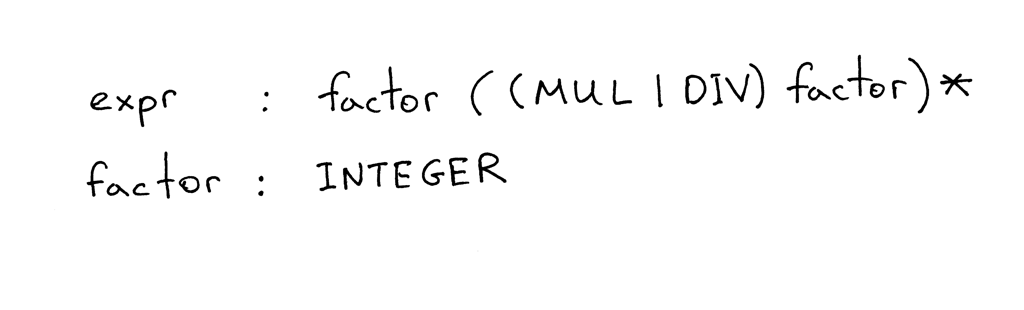
  1. 什么是上下文无关语法（语法）？
  2. 这个语法有几条规则/生成式？
  3. 什么是终结符？（指出图片中的所有终结符）
  4. 什么是非终结符？（指出图片中的所有非终结符）
  5. 什么是一条规则的 head？（指出图片中所有的 head/左边）
  6. 什么是一条规则的 body？（指出图片中所有的 body/右边）
  7. 什么是一个语法的开始符号？

哈，你从头读到了尾！这篇文章包含了不少理论，能看完它我很为你骄傲。

我下次回来会带来一篇新文章──保持关注也别忘了做练习，对你有好处。

下面是我推荐的帮助你学习解释器和编译器的一些书：

  1. Language Implementation Patterns: Create Your Own Domain-Specific and General Programming Languages (Pragmatic Programmers)
  2. Writing Compilers and Interpreters: A Software Engineering Approach
  3. Modern Compiler Implementation in Java
  4. Modern Compiler Design
  5. Compilers: Principles, Techniques, and Tools (2nd Edition)

顺便说一下，我还在写一本书“et’s Build A Web Server: First Steps”，解释了怎么从头 写一个基本的 Web 服务器。你可以从这里， 这里 和 这里 来感受一下这本书。

本系列的所有文章：

Last Updated 2018-05-26 Sat 14:12.
Render by hexo-renderer-org with Emacs 25.2.2 (Org mode 9.1.13)
0%